0引言
气体绝缘金属封闭开关 (GasInsulatedMetal— EnclosedSwitchgear,GIS)因其突出的绝缘性能和高可靠性等优点被广泛应用
[1]
。随着GIS设备体积减小,重量变轻,设备的故障量也在增多。盆式绝缘子作为 GIS设备中重要组成部分,起到了支撑金属导杆、隔离电位、气室密封隔气等作用
[2]
。GIS生产运输过程中会产生金属微粒,微粒运动会导致盆式绝缘子气固界面上电荷分布不均匀,十分容易引起沿面闪络甚至击穿故障,成为导致高压气体绝缘设备故障甚至供电系统放电事故的来源。
改善绝缘子电场分布的常用方法有两种,一是增大曲率半径,二是增加屏蔽环,两者都是通过改变盆式绝缘子的外观结构来达到改善电场分布的目的
[3]
。改变结构虽然一定程度上缓解了局部电场过高的问题,但调控效果有限,且会造成绝缘子结构复杂、难以制造、制造成本上升等问题。日本学者最早提出了功能梯度材料(FGM)的概念,并将功能梯度的概念应用于盆式绝缘子的电场强度优化,通过使绝缘子的介电常数呈梯度变化来改变其沿面电场。
近年来,大量学者对介电功能梯度绝缘子沿面电场分布进行了研究。文献[4]研究得出U型介电常数分布对电场强度降低效果显著;文献[5]通过数值模拟,引入了优化后的介电常数双层分布的绝缘子,并与传统单层绝缘子比较,发现双层介电常数提高了绝缘子击穿电压;文献[6]提出了多种介电参数分布方案,经过实际验证后得知,介电参数先减小后不变的分布方案电场优化效果最好;文献[7]通过拓扑优化对盆式绝缘子介电常数进行改变,控制介电常数最大值为100,优化后发现三结附近场强下降最大,下降程度达42%。本文通过COMSOL建立盆式绝缘子模型,由于交流电压下,盆式绝缘子电场主要与介电常数分布相关,所以本文主要通过调整介电常数来改善沿面电场,通过对介电常数进行迭代优化,得到绝缘子各处介电常数分布,并采用等差梯度的方法对其进行离散化处理,结果表明:介电常数迭代优化效果明显,盆式绝缘子表面电场强度有所下降,且明显分布相对均匀。
1电场优化仿真
1.1 仿真模型
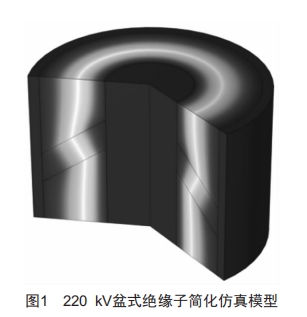
基于COMSOL软件对高压交流GIS模型进行电流场瞬态有限元仿真计算,建立二维轴对称模型,本文搭建的GIS盆式绝缘子简化模型如图1所示。
图1中,模型主要包括高压导体、金属外壳、盆式绝缘子。盆式绝缘子轴向厚度设置为30 mm,基体电导率为10~16S/m,介电常数设置为4。高压导体绝缘半径为40 mm,接地外壳半径为100 mm。运行时高压导杆通入220 kv、频率50 Hz交流电压,绝缘子外
壳接地。GIS内部空间充入SF6气体,电导率为10~20 S/m,介电常数设置为1。
1.2 介电功能梯度材料
功能梯度材料(FGM)通过使材料的化学构成沿某一方向发生渐变来满足材料各处性能不同的目的
[8]
。功能梯度材料的制备目前有层叠法、3D打印、离心制备等
[9]
。
设有两平行平板电极如图2所示。
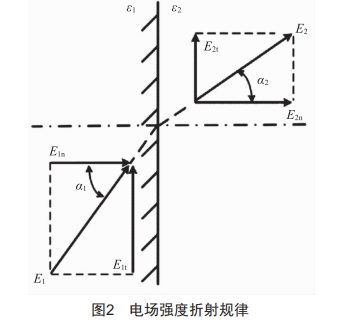
图2中,ε1、ε2分别为左右两侧平板的介电常数,E1、E2为左右两侧电场强度,α1为E1和分界面的夹角,α2为E2和分界面的夹角,分界面两侧的电通密度D的法向分量连续,电场强度E的切向分量连续
[10]
:
D
2n
=D
1n
(1)
E
1t
=E
2t
(2)
式中:D
1n
、D
2n
分别为左右分界面的电通密度;E
1t
、E
2t
分别为左右分界面的电场强度切向分量。
由于:
D
1n
=ε1E1 (3)
D
2n
=ε2E2 (4)
根据式(1)(2)可得E1sinα1=E2sinα2、ε1E1cosα1=ε2E2cosα2,两式相除,得:
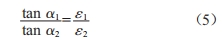
上述理论同样适用于盆式绝缘子。盆式绝缘子沿面电场强度最大的地方在其凹面侧,即高压导杆与凹面交界处。盆式绝缘子与同轴圆柱体电介质的电场优化类似,如图3所示,沿轴向方向将盆式绝缘子划分为多个同轴圆柱体,其中SF6 的介电常数为固定值,通过改变各个同轴圆柱体的介电常数来改变绝缘子沿面场强。
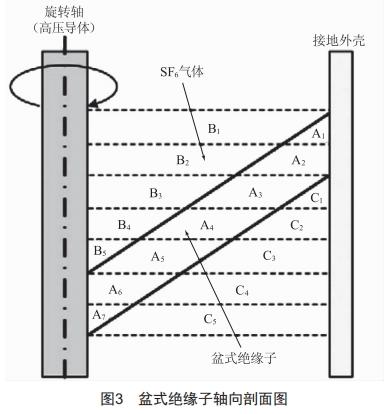
假设盆式绝缘子由m层不同电介质的同轴圆柱体串联而成,则当其工作在交流电压u时,其半径r
n
处的第n层同轴圆柱体上的最大场强En,max可由以下公式计算:
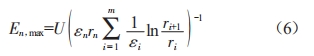
式中:εn为第n层的介电常数。且有:
ε1r1E1,max=ε2r2E2,max=…=εnrnEn,max (7)
由上式可得,通过改善材料的介电常数分布,可以达到改善电场的目的。
1.3 优化方法
本文通过迭代算法,对盆式绝缘子介电常数进行优化,初始介电常数设置为4,考虑到实际制作中环氧树脂的复合介质改性程度是有限的,介电常数约束范围取4~60。具体迭代过程如下:
1)首先在COMSOL中以当前的介电常数计算出盆式绝缘子沿面场强。
2)设置迭代结束条件为迭代次数达到5次,5次迭代后自动停止,否则,根据式(8)继续更新介电常数值,式中介电常数沿半径方向梯度分布。
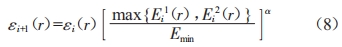
式中:εi+1 (r)为本轮迭代优化后绝缘子介电常数;εi (r)为当前盆式绝缘子上的介电常数;Ei1 (r)为绝缘子凸面沿面场强;Ei2 (r)为绝缘子凹面沿面场强;Emin为绝缘子参考场强最小值;α为收敛系数。
α越大,代表每次迭代优化对介电常数调整的幅度越大;α越小,代表对介电常数调整的幅度越小。α取值需谨慎,过大会引起超调,反之则会影响收敛速度,增大计算量。本文中取α=1。
3)得出迭代后介电常数,判断其是否在4~60范围内,若不在,则需根据式(9)对其进行缩放处理,而后重新计算沿面场强。
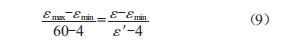
式中:εmax为缩放前介电常数最大值;εmin为缩放前介电常数最小值;ε为缩放前盆式绝缘子介电常数;ε/为缩放后盆式绝缘子介电数。
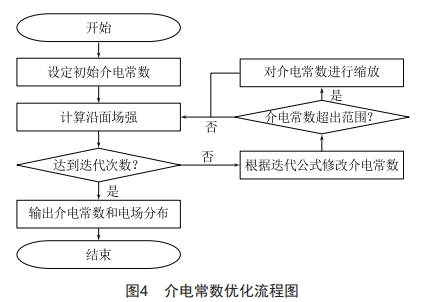
本文中设置介电常数最小为4,最大为60。图4为介电常数迭代流程。
2优化结果
2.1电场分布
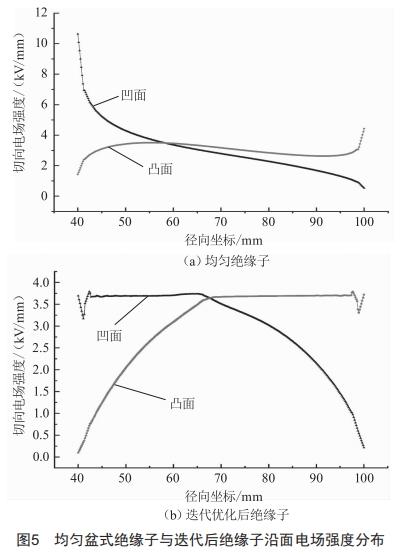
图5为盆式绝缘子优化前后的沿面场强分布。优化前,盆式绝缘子介电常数均匀为4,由图5(a)可看出,其凹面电场分布极不均匀,电场强度最大可达到10.626 kv/mm,位于高压导杆附近,此位置极易引发沿面闪络,最小电场强度为0.527 kv/mm,位于接地外壳附近;凸面电场分布相对凹面电场均匀,最大电场强度为4.423 kv/mm,最小电场强度为1.426 kv/mm。采用迭代优化算法优化过后,由图5(b)可看出,盆式绝缘子凹、凸两面最大场强均控制为3.792 kv/mm,最大电场强度下降幅度为64.3%。
迭代过程中,盆式绝缘子介电常数分布变化如图6所示。
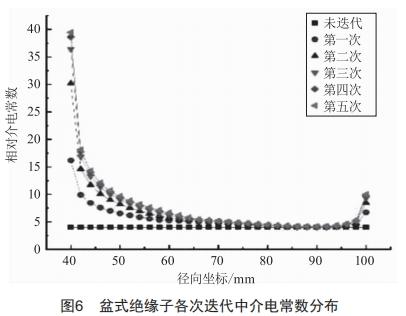
由图6可得,五次迭代过程中介电常数均未超过4~60,所以并未对其进行线性缩放。在第三次迭代后,相对介电常数就已经趋向收敛,优化后的介电常数分布趋势呈中间低、两头高。由于凹面电场强度高,为了降低此处电场强度,高压导杆附近介电常数相对较大;同样地,接地电极附近介电常数高是因为凸面电场强度最大值出现在此处。
2.2梯度离散化
实际工业制作中,介电常数连续分布的功能梯度绝缘子制作相对困难,可以通过对绝缘子进行等差梯度离散,利用层叠法或3D打印技术进行工业制作。
将介电常数均匀划分为多个区间,根据等差值的介电常数划分各个区间绝缘子的厚度,每层绝缘子介电常数取本区间内介电常数最大值
[11]
。本文中将介电常数划分为等差值的5个区间,图7为本文所采取的介电常数离散化方案。
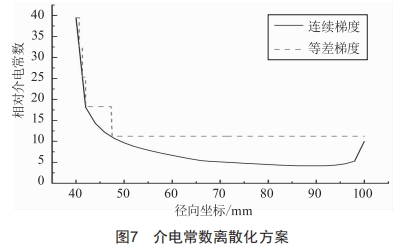
图8为等差离散后,盆式绝缘子的沿面电场分布,由图可知,在绝缘子介电常数跳变处,电场强度随之跳跃畸变。连续梯度下盆式绝缘子最大电场强度为3.792 kv/mm,等差梯度下盆式绝缘子最大电场强度为6.294kv/mm,绝缘子最大沿面场强相对上升,但相对于未迭代前匀质绝缘子来说,最大场强下降40.8%,盆式绝缘子迭代优化效果依然可观。
图8等差离散后绝缘子沿面电场分布
3 结论
本文建立了盆式绝缘子电场分布模型,提出了一种盆式绝缘子表面电场优化迭代算法,通过改变绝缘子各处的介电常数分布来调整其沿面电场,本算法变量少,优化效率高。主要结论如下:
1)优化前盆式绝缘子介电常数均匀分布,迭代优化五次后介电常数由高压电极附近到接地电极附近逐渐减小。迭代到第三次后介电常数开始收敛,介电常数最大值出现在高压导杆附近,最小值出现在接地电极附近。
2)优化前盆式绝缘子高压导杆附近沿面场强最大,接地电极附近沿面场强最小;优化后绝缘子沿面电场强度分布相对均匀;沿面最大电场强度也由优化前的10.626kv/mm降低到3.792kv/mm,下降幅度为64.3%。
3)对盆式绝缘子介电常数进行等差离散后,盆式绝缘子最大沿面场强为6.294 kv/mm,相对连续梯度来说有所上升,但相对未迭代之前,沿面电场下降40.8%,优化效果良好。
[参考文献]
[1]严璋,朱德恒.高电压绝缘技术[M].3版.北京:中国电力出版社,2019.
[2]XUE J Y,CHEN J H,DONG J H,et al.A novel sight For understanding surFace charging phenomena on downsized HVDC GIL spacers with non-uniForm conductivity [J].International Journal oF Electrical power & Energy Systems,2020,120: 105979.1—105979.12.
[3]孙西昌,彭宗仁,党镇平,等.特高压交流架空线路用复合绝缘子均压特性研究 [J].高压电器,2008,44 (6):527—530.
[4]KURIMOTO M ,KAI A ,KATO K , et al.Fabrication of permittivity graded materials for reducing electric stress on electrode surface[c]//conference Record of the 2008 IEEE International Symposium on Electricity lnsulation,2008 : 265—268.
[5]KATO K,KURIMOTO M,ADAcHI H,et al.Impulse breakdown characteristics of permittivity graded solid spacer in SF6 [c]// 2001 Annual Report conference on Electrical Insulation and Dielectric phenomena, 2001 :401—404.
[6]KATO K,KURIMOTO M,SHUMIYA H,et al.Application of functionally graded material for solid insulator in gaseous insulation system[J].IEEE Transactions on Dielectrics and Electrical lnsulation:A publ— ication of the IEEE Dielectrics and Electrical Insulation Society,2006, 13(2) : 362—372.
[7]LIU Z,LI W D,WANG Y B,et al.Topology optimization and 3D—printing fabrication feasibility of high voltage FGM insulator [c]// 2016 International conference on High Voltage Engineering and Application (IcHVE),2016 : 1188—1191.
[8]马涛,赵忠民,刘良祥,等.功能梯度材料的研究进展及应用前景[J].化工科技,2012,20(1):71—75.
[9]孙秋芹,郭晓和,张永涛,等.基于介电功能梯度材料的盆式绝缘子电场分布优化[J].湖南大学学报(自然科学版),2018,45(8):99—106.
[10]冯慈璋,马西奎.工程电磁场导论[M].北京:高等教育出版社,2007.
[11]梁虎成 ,杜伯学 , 陈允 ,等.基于迭代算法的功能梯度绝 缘子介电常数分布优化[J] . 电工技术学报 , 2020 , 35(17):3758—3764.
2024年第12期第6篇